Net present value (NPV) is a tool that can help you determine if an investment or project is worthwhile to undertake.
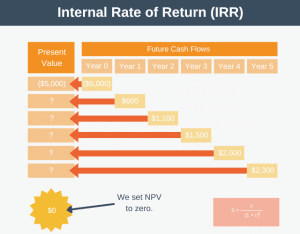
Imagine that you’re trying to decide if a project is worth doing. This project will require a one-off upfront cash investment of $5,000 and will return cash over five years as follows:
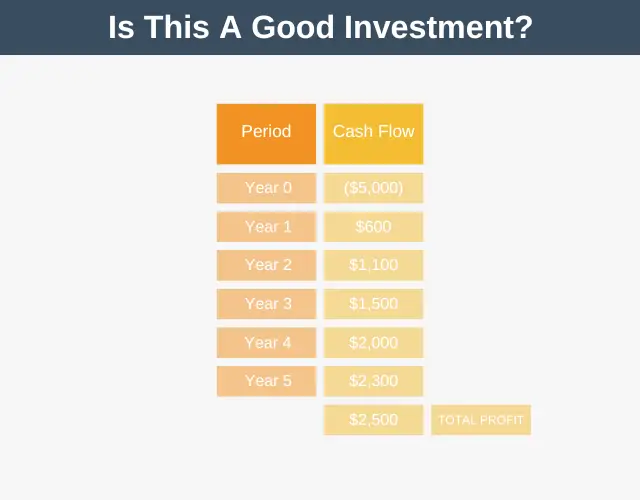
- Year 0: $(5,000) -> your initial investment
- Year 1: $600
- Year 2: $1,100
- Year 3: $1,500
- Year 4: $2,000
- Year 5: $2,300
As you can see, by investing $5,000 in this project, you estimate you’ll receive $7,500 in total over five years. So, the question is, “Is it worth taking on this project?”
At first glance, it might look like this project is worth doing because you’re making a 50% return ($7.5k return minus your $5k investment), but this thinking has a big problem.
Namely, the time value of money!
Over time money becomes less valuable for two reasons:
- Inflation.
- Opportunity Cost.
1. Inflation
Inflation erodes the purchasing power of money over time. In the 1980s, $1m would typically have bought you a 4,000-square-foot apartment in Manhattan. Today, that same $1m will buy you just an 876-square-foot apartment.
So it’s clear $1m was worth more 40 years ago than it is today, and it will be worth even less than it is today 40 years from now.
2. Opportunity Cost
Another reason you would prefer not to have the money 40 years from now is that you’re giving up the opportunity to do something with the money right now. With $1m now, you could use that money as you like today. Maybe you’d invest it or buy a place to live.
This phenomenon whereby time affects the value of money is called the time value of money, and it simply means that it’s better to receive a sum of money now than an identical sum at a later date.
Let’s return to our example and the question of whether it is worthwhile for us to invest $5k to receive $7.5k over five years? With this new information about the time value of money, maybe the investment case doesn’t look as positive as before, but how can we know for sure? This is where net present value comes in.
You can use net present value to discount future cash flows back to their current value. But what should you discount these future cash flows by?
The Discount Rate
The rate at which we discount future cash flows is called the discount rate. The discount rate is as simple as saying:
- To me, $10 today is worth just $9 next year, or
- To me, $10 today is worth just $7.50 next year.
Choosing a discount rate is a critical part of NPV, but it’s also a bit of a black art, and there is no right or wrong way to do it.
A couple of ways to think about the discount rate are:
- As the interest rate you could easily achieve if you invested your money elsewhere. For example, if you can earn a 5% yield on 10-year treasury bonds, you might set your discount rate to 5%.
- As the minimum acceptable rate of return, or hurdle rate, you’d like your investment to achieve. For example, maybe you don’t consider it worthwhile to take on any project that doesn’t earn you at least a 10% return, in which case you’d set your discount rate to 10%.
For our example, let’s set the discount rate to 10%. Now that we’ve set the discount rate, we’re finally able to calculate the net present value.
Present Value
The formula for calculating the present value of a single cash flow that you receive in the future is:

Note that this calculation computes the value of just one single future cash flow. The variables in this diagram are as follows:
- c = current cash flow
- r = the discount rate.
- t = the time interval defined in some unit. The unit can be any unit of time you like, so it could be years, which would mean that 0 = year zero, 1 = year one, 2 = year two, etc., or it could be months which would mean that 1 = month one and 7 = month seven.
Let’s use this formula to calculate the Net Present Value for our example.

The result of this is that you’ve calculated your NPV to be $376. How do you interpret your result of $376? Well, with NPV, if the result is above zero, then that means the investment is worth pursuing. Conversely, if the investment is less than zero, you are better off declining the investment.
Effectively, a value above zero tells us that our investment will clear our annual hurdle rate (or discount rate), which for our example, was 10%.
Net Present Value Formula
So far, the present value equation we’ve looked at shows how to calculate the present value of a single cash flow. In our example, we used that equation multiple times to calculate our net present value. Note that sometimes you will see this expressed as follows:
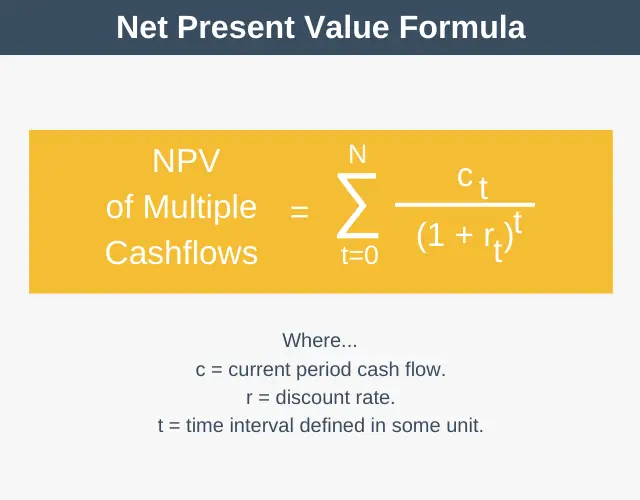
All this equation is saying is to do exactly as we did in our example – to sum all the present values together to work out our net present value. Note that the “t” next to the “r” in the equations means that it’s possible, if you want, to have a different discount rate for each time period.
Discount Rate vs. Discount Factors
One way to slightly speed up the calculation of net present value is to use discount factors. A discount factor is a decimal value you multiply your future cash flow by to calculate its present value.

The discount factor can be calculated by the formula:
- Discount factor = 1 / (1 * (1 + discount rate)^period number)
Where the discount rate and period number are used in the same way as in the net present value calculation.
However, most people don’t calculate the discount factor. This is because someone else has already done it and published it in table format. These published tables will look something like this:
| Period | 1% | 2% | 3% | 4% | 5% | 6% | 8% | 10% |
| 1 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 | 0.9434 | 0.9259 | 0.9091 |
| 2 | 0.9803 | 0.9612 | 0.9426 | 0.9246 | 0.9070 | 0.8900 | 0.8573 | 0.8265 |
| 3 | 0.9706 | 0.9423 | 0.9151 | 0.8890 | 0.8638 | 0.8396 | 0.7938 | 0.7513 |
| 4 | 0.9610 | 0.9239 | 0.8885 | 0.8548 | 0.8227 | 0.7921 | 0.7350 | 0.6830 |
| 5 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 | 0.7473 | 0.6806 | 0.6209 |
| 6 | 0.9421 | 0.8880 | 0.8375 | 0.7903 | 0.7462 | 0.7050 | 0.6302 | 0.5645 |
| 7 | 0.9327 | 0.8706 | 0.8131 | 0.7599 | 0.7107 | 0.6651 | 0.5835 | 0.5132 |
So all you have to do is quickly scan the table to see what your discount factor should be. For example, the discount factor for an 8% discount rate over five years would be 0.6806.
Using Excel and Google Sheets
By far, the quickest way to calculate net present value is to use a spreadsheet such as Excel or Google Sheets. To calculate the net present value, you use the NPV function, where you simply enter your discount rate followed by your cashflows, in turn.

Advantages and Disadvantages
There are several advantages and disadvantages associated with net present value.
Advantages
- NPV is easy to calculate.
- It allows you to compare one investment to another.
- It takes into account the time value of money when appraising investments.
Disadvantages
- You must select a discount rate, and there is no guidance on how to do this.
- NPV is not applicable in many situations, such as startups where it isn’t possible to estimate future cash flows.
- There is always the risk that your estimates for future cash flows are over-optimistic and your project fails to return as much as estimated. Some organizations use a margin of safety in their NPV calculations to compensate for this. For example, suppose an organization sets its margin of safety margin to 20%. In that case, they’d not authorize an investment unless the NPV value was not only above 0 but 20% or more of the initial outlay. This way they give themselves some wiggle room should their estimates not turn our as accurate as hoped.
Summary
Net present value is a tool that takes into account the time value of money to help you appraise if an investment or project is worth undertaking.